St. Venant Terms in SWMM 5 and how they change for Force Mainsby dickinsonre |
Autodesk Technologist with Information about Stormwater Management Model (SWMM) for watershed water quality, hydrology and hydraulics modelers (Note this blog is not associated with the EPA). You will find Blog Posts on the Subjects of SWMM5, ICM SWMM, ICM InfoWorks, InfoSWMM and InfoSewer.
Thursday, October 7, 2010
St. Venant Terms in SWMM 5
Orifice and Weir flow calculations
Note: Orifice and Weir Flow Computations
The orifice flow calculation proceeds as follows:
1. Initially and whenever the setting (i.e., the fraction opened) changes, flow coefficients for both orifice and weir behavior are computed as follows:
a. For side orifices:
Define Hcrit = h/2 where h is the opening height.
b. For bottom orifices:
i. For a circular orifice, compute area over length (i.e., circumference) as AL = h /4.
ii. For a rectangular orifice compute AL = h*w/(2*(h+w)) where w is the opening width.
iii. Compute Hcrit = Cd*AL/0.414 where Cd is the orifice discharge coefficient.
At step 1b, the critical head for the bottom orifice, where orifice flow turns into weir flow, is found by equating the result of the orifice equation to that of the weir equation
Cd*Area*sqrt(2g)*sqrt(Hcrit) = Cw*Length*sqrt(Hcrit)*Hcrit or
Hcrit = (Cd * Area) / (Cw/sqrt(2g) * Length) The value of Cw/sqrt(2g) for a sharp crested weir is 0.414.
c. Compute the flow coefficients (where A is the area of the opening):
Corif = A*sqrt(2g)*Cd
Cweir = A*sqrt(2g)*Cd*sqrt(Hcrit)
2. During flow routing, compute the degree of inlet submergence (f) and head (H) at the current time step:
a. Define:
H1 = upstream head (from node with higher head),
H2 = downstream head (from node with lower head) ,
Hcrest = elevation of bottom of opening,
Hcrown = elevation of top of opening,
Hmidpt = elevation of midpoint of opening
b. For side orifices:
f = min{1.0, (H1 - Hcrest) / (Hcrown - Hcrest)}
if f < 1.0 then H = H1 - Hcrest,
else if H2 < Hmidpt then H = H1 - Hmidpt
else H = H1 - H2
c. For bottom orifices:
if H2 > Hcrest then H = H1 - H2
else H = H1 - Hcrest
f = min{1.0, H/Hcrit}
3. Compute the flow through the orifice (Q):
if f < 1.0 then Q = Cweir*f^1.5
else Q = Corif*sqrt(H)
4: Villemonte correction
If f < 1.0 and H2 > Hcrest then:
r = (H2 - Hcrest) / (H1 - Hcrest)
Q = Q * (1 - r^1.5)^0.385
Weir Flow Computations
1. Weir head calculations
h1 = Upstream Node Depth + Upstream Invert Elevation
h2 = Downstream Node Depth + Downstream Invert Elevation
If h2 is greater than h1 then the flow is reversed and h2 = h1 and h1 = h2
Weir Crest = Upstream Node Invert Elevation + Weir Offset Depth
Head = h1 – Weir Crest
2. Center Weir flow for Transverse Weirs
Q = Cw * Weir Length * Head^3/2
3. Center Weir flow for Side Flow Weirs
Weir behaves as a transverse weir under reverse flow
Q = Cw * Weir Length * Head^3/2
And under normal flow
Q = Cw * Weir Length * Head^5/3
4. Center Weir flow for V Notch Weirs
Q = Cw * Weir Slope * Head^5/2
Wednesday, October 6, 2010
Tuesday, October 5, 2010
Saturday, October 2, 2010
SWMM 5 Pump Curve Head/Flow Curves (1)
1. The volume of the upstream wet well,
2. The depth of water at the upstream node or inlet node without interpolation between data points,
3. The downstream water surface elevation across the pump minus the upstream water surface elevation, and
4. The depth of water at the upstream node or inlet node with interpolation between data points.
The pump summary table in the rpt file will tell you how often the pump was used, the maximum flow, the average flow, the total volume of the pump, the power usage and the percent of the time off the entered pump curve. You can also plot the pump flow versus the inlet depth to see how often the pump was off the pump curve (Figure 2).
Figure 1: Plot of Head and Flow for Pump PUMP1@82309e-15009e over time along with the input and output table for the pump.
Figure 2: Plot of Head versus Flow for Pump PUMP1@82309e-15009e
Average Number of Node Iterations
Link Area Types in SWMM 5
Link Area Types in SWMM 5, InfoSWMM and H2OMap SWMMby dickinsonre |
Class
|
Description
|
Link Area Assignment
|
0 Dry conduit
|
1/2 Upstream and 1/2 Downstream Node
| |
1 Upstream end is dry
|
1/2 Downstream Node
| |
2 Downstream end is dry
|
1/2 Upstream Node
| |
3 Sub-critical flow
|
1/2 Upstream and 1/2 Downstream Node
| |
4 Super-critical flow
|
1/2 Upstream and 1/2 Downstream Node
| |
5 Free-fall at upstream end
|
1/2 Downstream Node
| |
6 Free-fall at downstream end
|
1/2 Upstream Node
| |
| Class | Description | Link Area Assignment |
| 0 Dry conduit | 1/2 Upstream and 1/2 Downstream Node | |
| 1 Upstream end is dry | 1/2 Downstream Node | |
| 2 Downstream end is dry | 1/2 Upstream Node | |
| 3 Sub-critical flow | 1/2 Upstream and 1/2 Downstream Node | |
| 4 Super-critical flow | 1/2 Upstream and 1/2 Downstream Node | |
| 5 Free-fall at upstream end | 1/2 Downstream Node | |
| 6 Free-fall at downstream end | 1/2 Upstream Node | |
Orifice Critical Depth for Separating Weir Flow from Orifice Flow for Bottom Outlet Orifices in SWMM5
The Critical height is the opening where weir flow turns into orifice flow. It equals (Co/Cw)*(Area/Length) where Co is the orifice coeff., Cw is the weir coeff/sqrt(2g), Area is the area of the opening, and Length = circumference of the opening. For a basic sharp crested weir, Cw = 0.414. All of the units are based on the internal SWMM 5 units of American Standard.
For a circular orifice the Critical Height is:
Critical Height = Orifice Discharge Coefficient / 0.414 * Orifice Opening / 4
For a rectangular orifice the Critical Height is:
Critical Height = Orifice Discharge Coefficient / 0.414 * (Orifice Opening*Width) / (2.0*(Orifice Opening+Width))
The Orifice Critical Depth changes dynamically as the orifice is opening and closing for a bottom outlet orifice. The critical depth separating the orifice weir flow from orifice flow for a side outlet orifice is the height of the orifice.
Note: Orifice Critical Depth
The Critical height is the opening where weir flow turns into orifice flow. It equals (Co/Cw)*(Area/Length) where Co is the orifice coeff., Cw is the weir coeff/sqrt(2g), Area is the area of the opening, and Length = circumference of the opening. For a basic sharp crested weir, Cw = 0.414. All of the units are based on the internal SWMM 5 units of American Standard.
For a circular orifice the Critical
Critical Height = Orifice Discharge Coefficient / 0.414 * Orifice Opening / 4
For a rectangular orifice the Critic
Critical Height = Orifice Discharge Coefficient / 0.414 * (Orifice Opening*Width) / (2.0*(Orifice Opening+Width))
The Orifice Critical Depth
|
Friday, October 1, 2010
The four cross sectional areas in a link of SWMM 5 and InfoSWMM
dq1 = Time Step * RoughFactor / Rwtd^1.333 * |Velocity|
The weighted area (Awtd) is used in the dq2 term of the St. Venant equation:
dq2 = Time Step * Awtd * (Head Downstream – Head Upstream) / Link Length
 |
| Possible Link Graph and Computational Variables |
 |
| The 4 Areas of a Link in SWMM 5 - Rising Limb |
 |
| The 4 Areas of a Link in SWMM 5 - Rising Limb and Falling Limb |
Three Depths in a Link in SWMM 5
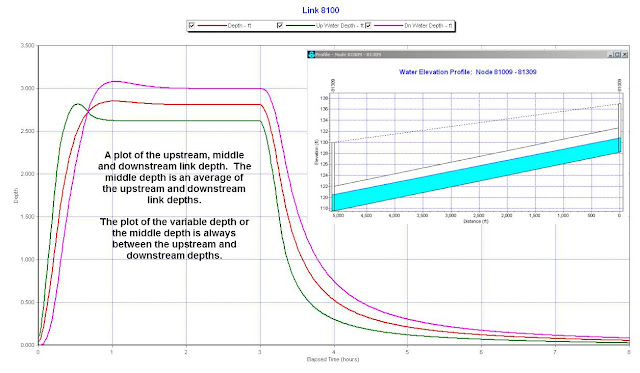
Note: An explanation of the three depths in a Link in SWMM 5 and a plot of the upstream, middle and downstream link depth. The middle depth is an average of the upstream and downstream link depths. The plot of the variable depth or the middle depth is always between the upstream and downstream depths. All three depths are used in the computation of the St. Venant Flow in SWMM 5. The upstream area is a function of the upstream depth and the downstream area is a function of the downstream depth.
The dq4 term in dynamic.c uses the area upstream (a1) and area downstream (a2), the midpoint velocity, the sigma factor (a function of the link Froude number), the link length and the time step or
dq4 = Time Step * Velocity * Velocity * (a2 – a1) / Link Length * Sigma
the dq3 term in dynamic.c uses the current midpoint area (a function of the midpoint depth), the sigma factor and the midpoint velocity
dq3 = 2 * Velocity * ( Amid(current iteration) – Amid (last time step) * Sigma
Time Base is T + T*K from the Time(T) and Storage (K) values
· The Fast UH has a time base of 22 hours,
· The Medium UH has a time base of 430 hours, and
· The Slow UH has a time base of 4212 hours.
If this is altered as in the bottom image you can see the difference in the total RDII I&I Flow
· The Fast UH has a time base of 22 hours,
· The Medium UH has a time base of 36 hours, and
· The Slow UH has a time base of 52 hours.
H2OMAP-Sewer - FM Split Issue
Note: One method would be to add a duplicate Wet Well/Pump/Force Main set of links to pass the flow from the upstream Force Main to the two downstream Force Mains (FM). The pump should be fixed capacity to handle all of the split GM flows. In this particular example the flows are split 50/50 to links 25 and 35 after leaving the loading manhole 24.
Pumps and Force Mains in InfoSWMM
Note: A pump is modeled in InfoSWMM somewhat akin to InfoSewer. You have a Wetwell connected to a Pump which in turn is connected to a Force Main. You can decide wheter a pipe is a Force Main or a Gravity Main by using the Atribute Browser and selecting Yes for Force Main and entering a FM Roughness.
You can also use the PickAx tool in the Attibrute Browser to convert the node from a Manhole to a WetWell / Storage node.
The Effect of the Hydrology Time Step on RDII Flow
Note: The wet hydrology time step and the report time step should be adjusted together to generate the smoothest RDII flow at your nodes. The three images show below show;
1. If you hydrology time step equals your rainfall time step then the RDII flow will have a step function appearance or your flows in this case will be constant for one hour or the rainfall interval,
2. If you choose a smaller hydrology time step then the flows will be smoother (2nd image), but
3. If the report time step is much less than the hydrology time step then the flows will still be stepwise linear for the hydrology time step size.
When picking a hydrology time step for continuous simulation you should probably pick a value of about 5 minutes so that the generated flows are smooth but not so small that a lot of time is used in the RDIi convolution process to generate the 3 units hydrographs for RDII.
Sunday, September 26, 2010
SWMM 5 Related Websites
MY BLOG LIST
- How to Use the SWMM 5 Excel Tool with InfoSewer CSV Files - How to Use the SWMM 5 Excel Tool with InfoSewer CSV Files 1. Export Link and Manholes in InfoSewer for your current Scenario to CSV files, 2. Set up the ...
4 minutes ago - Belgian potato chips? - What’s your favorite flavor of chips? Interestingly, both the potato and the term barbecue are indigenous to the Americas While not exactly a watershed-rel...
13 hours ago - 2D meshing – Avoiding small elements (and why this is so important) - When generating a 2D mesh in Innovyze products (such as InfoWorks ICM, CS 2D and InfoSWMM 2D) it is very important to avoid small mesh elements, as just on...
3 days ago - Increase in heavy rainfalls over past 60 years in upper Midwest, US - Increase in heavy rainfalls over past 60 years in upper Midwest, US http://www.sciencedaily.com/releases/2013/03/130313182312.htm March 14, 2013 Mar. 13...
4 months ago
Conduit Lengthening in SWMM 5
If you use the conduit lengthening option in SWMM 5 then your short conduits will be lengthened based on the CFL or explicit time step criterion. Any conduits in which the Length Factor or the courant time step link length over the original length is greater than 1 will be lengthened and will have its roughness lowered so that the conduit is hydraulically the same at full conduit depth. The full area, full width and full hydraulic radius stay the same in the modified link – only the length, slope and roughness are altered.
Length Factor = (Wave Celerity + Full Depth Velocity) * Time Step / Conduit Length, and for those links in which the Length Factor is greater than 1
New Roughness = Old Roughness / (Length Factor) ^1/2
New Slope = Old Slope / Length Factor
A few metric's for showing how this option has altered the network are shown in the figure below:
1. The most important is the increase in Network full volume as you never want to drastically alter the volume of your network,
2. The number of conduits modified along with the new mean slope (lower) and the new total conduit length are important indicators,
3. The mean wave celerity, full flow velocity and courant time step mean give the user some idea of the optimal time step for the simulation.
Mud Flow in SWMM 5
Tuesday, September 21, 2010
LPS Output Units when the Inflow is CMS
2. If you set the internal units to LPS in Run Manager,
3. Set the output units to LPS in Output Unit Manager,
4. Add a Scale multiplier of 1000 in the Inflows DB Table then
The inflows do not have to be altered, the internal model flows will LPS, the velocity will be m/s with 6 decimal places in the RPT file and the flows will be LPS with 3 decimal places in the RPT file.
Monday, September 20, 2010
Sunday, September 19, 2010
The Three Flows in SWMM 5 for a Link
There are actually three flows computed or used for a link in SWMM 5:
1. The St. Venant Flow equation flow
2. The Upstream Normal Flow Manning’s equation based on the link roughness, slope, upstream cross sectional area and upstream hydraulic Radius,
3. The flow actually used in the model which is either the flow computed from St. Venant or Manning’s equation
The following three links shows how this works in a real model:
· Link 8040 almost always uses the St. Venant Equation because it is dominated by backwater and surcharge
· Link 8100 almost always uses Manning’s equation except at the beginning and end of the simulation,
· Link 1600 is an adverse slope link and it mainly uses the St. Venant equation.
· Flow = the flow actually used during the simulation
· Qdynamic = the flow computed from the St. Venant Equation
· QNormUp = Flow based on Manning's equation at the upstream end of the link.
· QNormDown = Flow based on Manning's equation at the downstream end of the link.
Link 8100 almost always uses Manning’s equation except at the beginning and end of the simulation. The beginning and end of the simulation is when the non linear terms dominant.
Orifice Open and Close Speed and the Target Setting in SWMM 5
In SWMM 5 there is an orifice parameter called setting which opens or closes the orifice opening by modifying the depth of the orifice. The setting is based either on a RTC rule of the orifice or the Flap Gate condition of the orifice and can be between 0 and 1. Closed is 0; Open is 1. The difference is that the target setting is what the setting should be based on the condition of the Flap Gate or the RTC Rules and the setting is the value actually used in the model.
The open and close speed of the orifice modifies the orifice setting by changing the orifice setting based on the open and closing speed using the equation:
New Orifice Setting = Old Orifice Setting + (Target Setting – Orifice Setting) * Time Step / Orifice Open and Close Speed
If your target setting and the current orifice setting are both 1 or 0 then the orifice Open and Close option does not change the orifice setting. New Setting equals Old Setting in that case. If the target and setting are out of phase then the Open and Close Option will function correctly. For example, if the Open and Close Speed is 1 hour then the orifice setting will open and close in a one hour period. The table shown below shows how the orifice setting changes as a function of the speed and the difference between the target and orifice settings. The setting starts out open but the target says closed – the orifice then closes over a 1 hour period. At one hour the target setting is 1 and the orifice will then open over a one hour period.
Table - Link OR1@82309b-15009b
Setting Target
Days Hours
0 00:00:00 1.00 0.00
0 00:15:00 0.74 0.00
0 00:30:00 0.50 0.00
0 00:45:00 0.25 0.00
0 01:00:00 0.00 0.00
0 01:15:00 0.25 1.00
0 01:30:00 0.50 1.00
0 01:45:00 0.75 1.00
0 02:00:00 1.00 1.00
0 02:15:00 0.75 0.00
0 02:30:00 0.50 0.00
0 02:45:00 0.25 0.00
0 03:00:00 0.00 0.00
0 03:15:00 0.00 0.00
0 03:30:00 0.00 0.00
0 03:45:00 0.00 0.00
Example rule for the opening and closing of the orifice
RULE Orifice1
IF SIMULATION CLOCKTIME >= 01:00:00
AND SIMULATION CLOCKTIME <= 2:00:00
THEN ORIFICE OR1@82309b-15009b SETTING = 1
ELSE ORIFICE OR1@82309b-15009b SETTING = 0
PRIORITY 1
; Opens up the orifice at hour 1 of the simulation
Saturday, September 18, 2010
SWMM 5 Link Time Step Calculations
Thursday, September 16, 2010
Tuesday, September 14, 2010
Graphical Representation of Results in InfoSWWM
If you are using the report manager then you select the graphing by changing the From and To dates.
Saturday, September 11, 2010
SWMM 5 Interface Guide Tips for C Compilers
SWMM 5 has a Interfacing guide on http://www.epa.gov/nrmrl/wswrd/wq/models/swmm/#Downloads for creating a VB, Delphi or command line C program to both run and printout some of the output file results from SWMM 5. The readme file is self explanatory in the file http://www.epa.gov/nrmrl/wswrd/wq/models/swmm/swmm5_iface.zip but here are a few tips for those of you who want to compile the InterFaceGuide C code in a Executable file for Windows.
1. The first step is to make a new console program in Visual Studio
2. The second step is to add the files swmm5.h, swmm5_iface.h, swmm5_iface.c, test.c to the project header and source files.
3. Next add the file swmm5.lib as an additional dependency along with the directory name.
4. If you want to save the .out and .rpt files then you must comment out the remove statements at the end of test.c
5. You need to make a batch file to both run and save the input and output files from SWMM 5,
6. The file swmm5.dll must be in the same directory as the created interface executable file,
7. It will help you see the intermediate output if you add a pause statement in the batch file to hold the fprintf statements on the screen for you to view.
Weather Underground to SWMM 5 Rainfall Time Series
DWF Scale Factor in SWMM 5 for entering Population Data
Sunday, July 4, 2010
SWMM5 Routing Time Step Summary
The minimum time step is the smallest time step used during the simulation.The average time step is the mean time step used during the simulation.The maximum time step is the maximum time used during the simulation.The percent in steady state is the percent of the total simulation time spent in steady state during the simulation.The average iterations per time step is the total number of iterations during the simulation divided by the total number of time steps or step count in this table. This will range between 2 and 4 iterations as SWMM 5.0.018 has a minimum of 2 and and a maximum of 4 iterations.The Step count is the total number of time steps during the simulation.The percent of bypassed links are the link flows that are NOT computed between time step iteration 2 and 4 because both the upstream and downstream node depths are converged in the current time step.The percent of bypassed nodes are those nodes that have been converged between time step iteration 2 and 4. The node depth is still calculated, however, between iterations 2 and 4 as long as the whole time step is not considered converged.
Saturday, July 3, 2010
Explicit Iteration Hydraulic Computation and Implicit Time Step Hydraulic Computations in SWMM 5
Friday, March 19, 2010
Steady State Option in SWMM 5
Checking this option will make the simulation use the most recently computed conveyance system flows during a steady state period instead of computing a new flow routing solution. A time step is considered to be in steady state if the change in external inflow at each node is below 0.5 cfs and the relative difference between total system inflow and outflow is below 5%.
AI Rivers of Wisdom about ICM SWMM
Here's the text "Rivers of Wisdom" formatted with one sentence per line: [Verse 1] 🌊 Beneath the ancient oak, where shadows p...
-
@Innovyze User forum where you can ask questions about our Water and Wastewater Products http://t.co/dwgCOo3fSP pic.twitter.com/R0QKG2dv...
-
Subject: Detention Basin Basics in SWMM 5 What are the basic elements of a detention pond in SWMM 5? They are common in our back...
-
Soffit Level ( pipe technology ) The top point of the inside open section of a pipe or box conduit. The soffit is the ...


.png)



.png)
.png)





.png)


